Question

According to the Bureau of Labor Statistics, 7.1% of the labor force in Wenatchee, Washington was unemployed in February 2019. A random sample of 100 employable adults in Wenatchee, Washington was selected. Using the normal approximation to the binomial distribution, what is the probability that 6 or more people from this sample are unemployed

Answer 1

73.24% probability that 6 or more people from this sample are unemployed

Explanation:

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

Can be approximated to a normal distribution, using the expected value and the standard deviation.

The expected value of the binomial distribution is:

`E(X) = np`

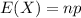
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

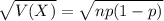
Normal probability distribution

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

When we are approximating a binomial distribution to a normal one, we have that
`\mu = E(X)`,
`\sigma = √(V(X))`.

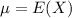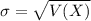In this problem, we have that:

`n = 100, p = 0.071`

So

`\mu = E(X) = np = 10*0.071 = 7.1`

`√(V(X)) = √(np(1-p)) = √(100*0.071*0.929) = 2.5682`

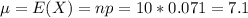
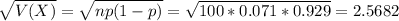
What is the probability that 6 or more people from this sample are unemployed

Using continuity correction, this is
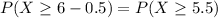`P(X \geq 6 - 0.5) = P(X \geq 5.5)`, which is 1 subtracted by the pvalue of Z when X = 5.5. So

`Z = (X - \mu)/(\sigma)`

`Z = (5.5 - 7.1)/(2.5682)`

`Z = -0.62`

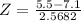
`Z = -0.62` has a pvalue of 0.2676

1 - 0.2676 = 0.7324

73.24% probability that 6 or more people from this sample are unemployed