Question

A tank contains 70 lb of salt dissolved in 400 gallons of water. A brine solution is pumped into the tank at a rate of 4 gal/min; it mixes with the solution there, and then the mixture is pumped out at a rate of 4 gal/min. Determine A(t), the amount of salt in the tank at time t, if the concentration of salt in the inflow is variable and given by cin(t)

Answer 1

`A(t)=400C_(in)(t)+[70-400C_(in)(t)]\cdot e^{-(t)/(100)}`

Explanation:

Volume of water in the Tank =400 gallons

Let A(t) be the amount of salt in the tank at time t.

Initially, the tank contains 70 lbs of salt, therefore:

A(0)=70 lbs

Amount of Salt in the Tank

`(dA)/(dt)=R_(in)-R_(out)`

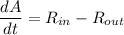
=(concentration of salt in inflow)(input rate of brine)

`=(C_(in)(t))( 4(gal)/(min))\\=4C_(in)(t)(lbs)/(min)`

=(concentration of salt in outflow)(output rate of brine)

`=((A(t))/(400))( 4(gal)/(min))=(A)/(100)`

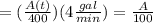
Therefore:

`(dA)/(dt)=4C_(in)(t)-(A)/(100)`

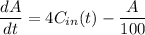
We then solve the resulting differential equation by separation of variables.

`(dA)/(dt)+(A)/(100)=4C_(in)(t)\\$The integrating factor: e^{\int (1)/(100)}dt =e^{(t)/(100)}\\$Multiplying by the integrating factor all through\\(dA)/(dt)e^{(t)/(100)}+(A)/(100)e^{(t)/(100)}=4C_(in)(t)e^{(t)/(100)}\\(Ae^{(t)/(100)})'=4C_(in)(t)e^{(t)/(100)}`

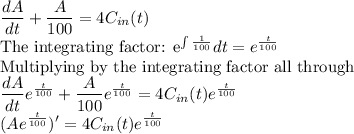
Taking the integral of both sides

`\int(Ae^{(t)/(100)})'=\int [4C_(in)(t)e^{(t)/(100)}]dt\\Ae^{(t)/(100)}=4*100C_(in)(t)e^{(t)/(100)}+C, $(C a constant of integration)\\Ae^{(t)/(100)}=400C_(in)(t)e^{(t)/(100)}+C\\$Divide all through by e^{(t)/(100)}\\A(t)=400C_(in)(t)+Ce^{-(t)/(100)}`

Recall that when t=0, A(t)=70 lbs (our initial condition)

`A(t)=400C_(in)(t)+Ce^{-(t)/(100)}\\</p><p>70=400C_(in)(t)+Ce^{-(0)/(100)}\\</p><p>C=70-400C_(in)(t)\\$Therefore, the amount of salt in the tank at any time t is:</p><p>\\\\A(t)=400C_(in)(t)+[70-400C_(in)(t)]\cdot e^{-(t)/(100)}`