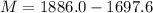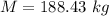Question

A spherical balloon has a radius of 7.40 m and is filled with helium. Part A How large a cargo can it lift, assuming that the skin and structure of the balloon have a mass of 990 kg ? Neglect the buoyant force on the cargo volume itself. Assume gases are at 0∘C and 1 atm pressure (rhoair = 1.29 kg/m3, rhohelium = 0.179 kg/m3).

Answer 1

The mass of the cargo is
`M = 188.43 \ kg`

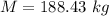
Step-by-step explanation:

From the question we are told that

The radius of the spherical balloon is
`r = 7.40 \ m`

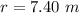
The mass of the balloon is
`m = 990\ kg`

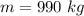
The volume of the spherical balloon is mathematically represented as

`V = (4)/(3) * \pi r^3`

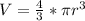
substituting values

`V = (4)/(3) * 3.142 *(7.40)^3`

`V = 1697.6 \ m^3`

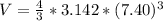
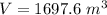
The total mass the balloon can lift is mathematically represented as

`m = V (\rho_h - \rho_a)`

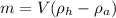
where
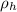`\rho_h` is the density of helium with a value of

`\rho_h = 0.179 \ kg /m^3`

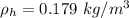
and
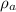`\rho_a` is the density of air with a value of

`\rho_ a = 1.29 \ kg / m^3`

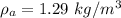
substituting values

`m = 1697.6 ( 1.29 - 0.179)`

`m = 1886.0 \ kg`

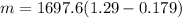
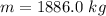
Now the mass of the cargo is mathematically evaluated as

`M = 1886.0 - 1697.6`

`M = 188.43 \ kg`