Question

A coaxial cable consists of a thin insulated straight wire carrying a current of 2.00 A surrounded by a cylindrical conductor carrying a current of 3.50 A in the opposite direction. The cylindrical conductor has a radius of 0.420 cm. What is the magnitude of the magnetic field outside of the cylindrical conductor 2.00 cm from the central wire

Answer 1

B = 15μT

Step-by-step explanation:

In order to calculate the magnitude of the magnetic field generated by the coaxial cable you use the Ampere's law, which is given by:

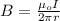`B=(\mu_oI)/(2\pi r)` (1)

μo: magnetic permeability of vacuum = 4π*10^-7 T/A

I: current

r: distance from the wire to the point in which B is calculated

In this case you have two currents with opposite directions, which also generates magnetic opposite magnetic fields. Then, you have (but only for r > radius of the cylindrical conductor) the following equation:

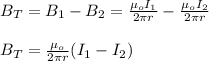`B_T=B_1-B_2=(\mu_o I_1)/(2\pi r)-(\mu_o I_2)/(2\pi r)\\\\B_T=(\mu_o)/(2\pi r)(I_1-I_2)` (2)

I1: current of the central wire = 2.00A

I2: current of the cylindrical conductor = 3.50A

r: distance = 2.00 cm = 0.02 m

You replace the values of all parameters in the equation (2), and you use the absolute value because you need the magnitude of B, not its direction.

`|B|=|(4\pi*10^(-7)T/A)/(2\pi (0.02m))(2.00A-3.50A)|=1.5*10^(-5)T\\\\|B|=15*10^(-6)T=15\mu T`

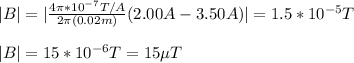
The agnitude of the magnetic field outside the coaxial cable, at a distance of 2.00cm to the center of the cable is 15μT