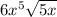Question:
Which is equivalent to
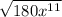 after it has been simplified completely?
after it has been simplified completely?
Answer:
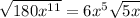
Explanation:
Given
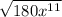
Required
Simplify
We start by splitting the square root
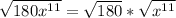
Replace 180 with 36 * 5
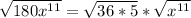
Further split the square roots
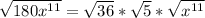
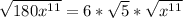
Replace power of x; 11 with 10 + 1

From laws of indices;
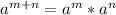
So, we have

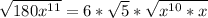
Further split the square roots
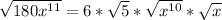
From laws of indices;
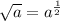
So, we have
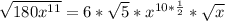
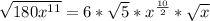
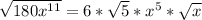
Rearrange Expression
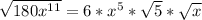
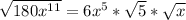
From laws of indices;
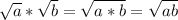
So, we have
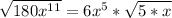
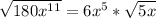
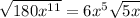
The expression can no longer be simplified
Hence,
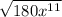 is equivalent to
is equivalent to