Question

A mass of 5.00 kg pulls down vertically on a string that is wound around a rod of radius 0.100 m and negligible moment of inertia. The rod is fixed in the center of a disk. The disk has mass 125 kg and radius 0.2 m. They turn freely about a fixed axis through the center. What is the angular acceleration of the rod, in radians/s 2

Answer 1

0.981 rad/sec^2

Step-by-step explanation:

mass that pulls on string = 5 kg

weight due to mass = 5 x 9.81 = 49.05 N

radius of rod = 0.1 m

torque produced by this force on the rod = force x radius

torque = 49.05 x 0.1 = 4.905 N-m

mass of disk = 125 kg

radius of disk = 0.2 m

moment of inertia of the disk I = m
`r^(2)`

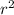
I = 125 x
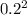`0.2^(2)` = 5 kg-m^2

from the equation, T = Iα

where T is torque

I is moment of inertia

α is angular acceleration

imputing values,

4.905 = 5α

α = 4.905/5 = 0.981 rad/sec^2