Answer:
The maximum speed v that the car can go without flying off the track = 15.29 m/s
Step-by-step explanation:
let us first lay out the information clearly:
mass of car (m) = 410 kg
radius of race track (r) = 83.4 m
coefficient of friction (μ) = 0.286
acceleration due to gravity (g) = 9.8 m/s²
maximum speed = v m/s
For a body in a constant circular motion, the centripetal for (F) acting on the body is given by:
F = mass × ω
where:
F = maximum centripetal force = mass × μ × g
ω = angular acceleration =
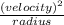
∴ F = mass × ω
m × μ × g = m ×

410 × 0.286 × 9.8 = 410 ×
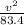
since 410 is on both sides, they will cancel out:
0.286 × 9.8 =
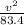
2.8028 =
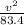
now, we cross-multiply the equation
2.8028 × 83.4 =

 = 233.754
= 233.754
∴ v = √(233.754)
v = 15.29 m/s
Therefore, the maximum speed v that the car can go without flying off the track = 15.29 m/s