Answer:
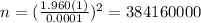
So the answer for this case would be n=384160000 rounded up to the nearest integer
Explanation:
We know the following info:
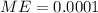 represent the margin of error desired
represent the margin of error desired
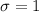 we assume that the population deviation is this value
we assume that the population deviation is this value
The margin of error is given by this formula:
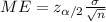 (a)
(a)
And on this case we have that ME =0.0001 and we are interested in order to find the value of n, if we solve n from equation (a) we got:
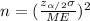 (b)
(b)
The critical value for 95% of confidence interval now can be founded using the normal distribution. If we use the normal standard distribution or excel we got:
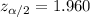 , replacing into formula (b) we got:
, replacing into formula (b) we got:
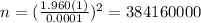
So the answer for this case would be n=384160000 rounded up to the nearest integer