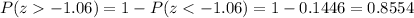Question

A carpet expert believes that 8% of Persian carpets are counterfeits. If the expert is accurate, what is the probability that the proportion of counterfeits in a sample of 827 Persian carpets would be greater than 7%

Answer 1

`z=(0.07-0.08)/(0.00943)= -1.06`

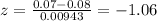
And we can use the normal standard distribution table and the cmplement rule and we got:

`P(z>-1.06) = 1- P(z<-1.06) = 1-0.1446= 0.8554`

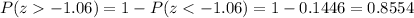
Explanation:

For this case we know the following info given:

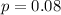`p=0.08` represent the population proportion

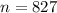`n= 827` represent the sample size selected

We want to find the following proportion:

`P(\hat p>0.07)`

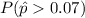
For this case we can use the normal approximation since we have the following conditions:

i) np = 827*0.08 = 66.16>10

ii) n(1-p) = 827*(1-0.08) =760.84>10

The distribution for the sample proportion would be given by:

`\hat p \sim N (p ,\sqrt{(p(1-p))/(n)})`

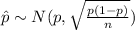
The mean is given by:

`\mu_(\hat p)= 0.08`

And the deviation:

`\sigma_(\hat p)= \sqrt{(0.08*(1-0.08))/(827)}= 0.00943`

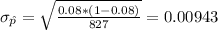
We can use the z score formula given by:

`z=(\hat p -\mu_(\hat p))/(\sigma_(\hat p))`

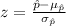
And replacing we got:

`z=(0.07-0.08)/(0.00943)= -1.06`

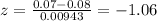
And we can use the normal standard distribution table and the cmplement rule and we got:

`P(z>-1.06) = 1- P(z<-1.06) = 1-0.1446= 0.8554`