Answer:
The mass of the second block is 0.94 kg
Step-by-step explanation:
Given;
mass of the first block, m₁ = 0.47 kg
let the mass of the first block and second block = m₂
According to Hook's law;
F = kx
where;
F is the applied load (force)
k is the elastic constant
x is the extension of the elastic material
According to Newton's law of motion;
F = ma = mg
Thus,
mg = kx
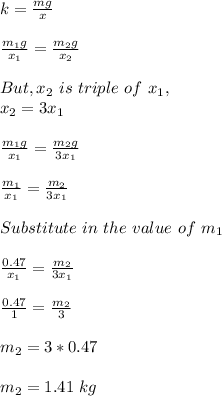
mass of the second block alone = 1.41 - 0.47 = 0.94 kg
Therefore, the mass of the second block is 0.94 kg