Question

The initial kinetic energy imparted to a 0.25 kg bullet is 1066 J. The acceleration of gravity is 9.81 m/s 2 . Neglecting air resistance, find the range of this projectile when it is fired at an angle such that the range equals the maximum height attained. Answer in units of km.

Answer 1

The range of the bullet is 0.435 kilometers.

Step-by-step explanation:

According to the problem, maximum height is equal to the range of the bullet. That is:

`\Delta x = \Delta y`

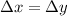
Where:

`\Delta x` - Range of the bullet, measured in meters.

`\Delta y` - Maximum height of the bullet, measured in meters.

By the Principle of Energy Conservation, gravitational potential energy reaches its maximum at the expense of the initial kinetic energy. That is to say:

`K_(1) = U_(2)`

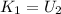
Where:

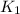`K_(1)` - Kinetic energy at point 1, measured in joules.

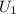`U_(1)` - Gravitational potential energy at point 2, measured in joules, and:

`U_(2) = m\cdot g \cdot \Delta y`

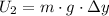
Where:

`m` - Mass of the bullet, measured in kilograms.

`g` - Gravitational constant, measured in meters per square second.

The maximum height is now cleared:

`K_(1) = m\cdot g \cdot \Delta y`

`\Delta y = (K_(1))/(m\cdot g)`

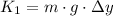
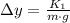
If
`K_(1) = 1066\,J`,
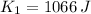`m = 0.25\,kg` and
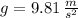`g = 9.81\,(m)/(s^(2))`, the maximum height is now computed:

`\Delta y = (1066\,J)/((0.25\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right))`

`\Delta y = 434.791\,m`

`\Delta y = 0.435\,km`

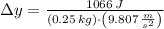
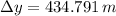
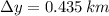
Lastly, the range of the bullet is 0.435 kilometers.