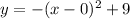Question

Select the correct answer. This graph represents a quadratic function. What is the value of a in this function’s equation? A)-1 B)2 C)1 D)-2

Answer 1

Explanation:

We will use the work form of a quadratic to determine what a is...in fact we will write the equation for the whole thing in the process, because it's part of solving for a.

y = ±|a|(x - h)² + k

where x and y are from a coordinate point on the graph, h and k are the coordinates of the vertex, the absolute value of a indicates how steep or flat the graph is compared to the parent graph, and the ± is because a positive parabola opens up and a negative one opens upside down.

The vertex is (0, 9) and the coordinate point I chose to use is (3, 0). Filling those in and solving for a:

0 = ±|a|(3 - 0)² + 9 and

0 = ±|a|(3)² + 9 and

-9 = ±|a|9 and

-1 = ±|a| so a = 1. Because this is an upside down parabola the negative is out front, but a is independent of it. The correct choice is C. The quadratic function is

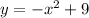`y=-x^2+9` or in more detailed form:

`y=-(x-0)^2+9`

Answer 2

-2

Explanation: