Question

In a hydroelectric power plant, water enters the turbine nozzles at 800 kPa absolute with a low velocity. If the nozzle outlets are exposed to atmospheric pressure of 100 kPa, determine the maximum velocity (m/s) to which water can be accelerated by the nozzles before striking the turbine blades.

Answer 1

The answer is VN =37.416 m/s

Step-by-step explanation:

Recall that:

Pressure (atmospheric) = 100 kPa

So. we solve for the maximum velocity (m/s) to which water can be accelerated by the nozzles

Now,

Pabs =Patm + Pgauge = 800 KN/m²

Thus

PT/9.81 + VT²/2g =PN/9.81 + VN²/2g

Here

Acceleration due to gravity = 9.81 m/s

800/9.81 + 0

= 100/9.81 + VN²/19.62

Here,

9.81 * 2= 19.62

Thus,

VN²/19.62 = 700/9.81

So,

VN² =1400

VN =37.416 m/s

Note: (800 - 100) = 700

Answer 2

`V2 = 37.417ms^(-1)`

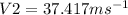
Step-by-step explanation:

Given the following data;

Water enters the turbine nozzles (inlet) = 800kPa = 800000pa.

Nozzle outlets = 100kPa = 100000pa.

Density of water = 1000kg/m³.

We would apply, the Bernoulli equation between the inlet and outlet;

`(P_(1) )/(d)+(V1^(2) )/(2) +gz_(1) = (P_(2) )/(d)+(V2^(2) )/(2) +gz_(2)`

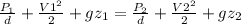
Where, V1 is approximately equal to zero(0).

Z
`z_(1) = z_(2)`

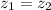
Therefore, to find the maximum velocity, V2;

`V2 = \sqrt{2((P_(1) )/(d)-(P_(2) )/(d)) }`

`V2 = \sqrt{2((800000)/(1000)-(100000)/(1000)) }`

`V2 = √(2(800-100))`

`V2 = √(2(700))`

`V2 = √(1400)`

`V2 = 37.417ms^(-1)`

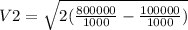
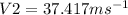
Hence, the maximum velocity, V2 is 37.417m/s