Question

Please help :( Algebra 2 Question

A child arranges toy action figures into rows. The first row has three action figures and each row after the first has six more figures than the row before it. Write a rule for the number of action figures in the nth row. If there are nine , how many action figures are there?

Answer 1

number of action figures = 3 + 6(n-1)

at n = 9: number of action figures = 51

Explanation:

first row: 3

second row: 6 more than the row before it (3) = 6 + 3 = 9

third row: 6 + 9 = 15

arithmetic series:
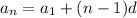`a_n = a_1 + (n-1)d`, where

`a_n` is the nth term in the output

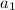`a_1` is the first output

n is the input

d is the difference between terms

here, we are given the row, and we want to figure out the number of action figures. thus, row = input and number of action figures = output.

the first output, in the first row, is 3

the difference between the number of action figures in each row is 6

thus, our formula is

`a_n = 3 + (n-1)6 = 3 + 6(n-1)`

when the row is 9, the number of action figures is equal to

3 + 6(9-1) = 3 + 6 * 8 = 51