Question

Help me please…………………………

Answer 1

Correct option: First one ->
`x^2 = -12y`

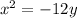
Explanation:

The focus and the vertex have the same x-coordinate, so we have a vertical parabola. The standard equation for this parabola is:

`y = a(x-h)^2 + k`

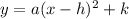
If the vertex is at the origin, we have that:

`(h, k) = (0,0)\\h = 0, k = 0`

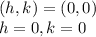
If the focus is at (0,-3), we have that:

`(h, k+p) = (0, -3)`

`p = 1/4a`

`k + p = -3`

`1/4a = -3`

`a = -1/12`

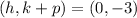
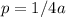
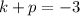
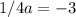
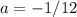
So we equation of the parabola is:

`y = -x^2/12`

`x^2 = -12y`

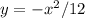
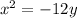
Correct option: First one