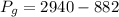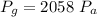Question

A tall cylinder contains 30 cm of water. Oil is carefully poured into the cylinder, where it floats on top of the water, until the total liquid depth is 40 cm. Part A What is the gauge pressure at the bottom of the cylinder

Answer 1

The gauge pressure is
`P_g = 2058 \ P_a`

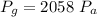
Step-by-step explanation:

From the question we are told that

The height of the water contained is
`h_w = 30 \ cm = 0.3 \ m`

The height of liquid in the cylinder is
`h_t = 40 \ cm = 0.4 \ m`

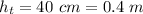
At the bottom of the cylinder the gauge pressure is mathematically represented as

`P_g = P_w + P_o`

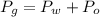
Where
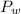`P_w` is the pressure of water which is mathematically represented as

`P_w = \rho_w * g * h_w`

Now
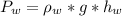
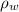`\rho_w` is the density of water with a constant values of
`\rho_w = 1000 \ kg /m^3`

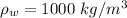
substituting values

`P_w = 1000 * 9.8 * 0.3`

`P_w = 2940 \ Pa`

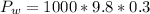
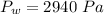
While
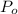`P_o` is the pressure of oil which is mathematically represented as

`P_o = \rho_o * g * (h_t -h_w )`

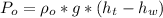
Where
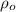`\rho _o` is the density of oil with a constant value

`\rho _o = 900 \ kg / m^3`

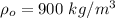
substituting values

`P_o = 900 * 9.8 * (0.4 - 0.3)`

`P_o = 882 \ Pa`

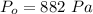
Therefore

`P_g = 2940 - 882`

`P_g = 2058 \ P_a`