Question

Water flowing out of a horizontal pipe emerges through a nozzle. The radius of the pipe is 1.8 cm, and the radius of the nozzle is 0.53 cm. The speed of the water in the pipe is 0.75 m/s. Treat the water as an ideal fluid, and determine the absolute pressure of the water in the pipe.

Answer 1

The absolute pressure of the water in the pipe is 1.38 x 10⁵ Pa

Step-by-step explanation:

Given;

radius of the pipe, r₁ = 1.8 cm = 0.018 m

radius of the pipe, r₂ = 0.53 cm = 0.0053 m

speed of water in the pipe, v₁ = 0.75 m/s

Water absolute pressure can be determined using Bernoulli's equation;

P₁ + ¹/₂ρv₁² = P₂ + ¹/₂ρv₂²

P₁ = P₂ + ¹/₂ρv₂² - ¹/₂ρv₁²

P₁ = P₂ + ¹/₂ρ (v₂² - v₁²)

where;

ρ is density of water = 1000 kg/m³

P₂ is atmospheric pressure = 1.01 x 10⁵ Pa

From continuity equation; A₁V₁ = A₂V₂

πr₁²v₁² = πr₂²v₂²

`v_2 = ( r_1^2v_1)/(r_2^2)`

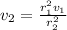
`P_1 = P_2 + (1)/(2) \rho[((r_1^2v_1)/(r_2^2) )^2 - v_1^2]\\\\P_1 = P_2 + (1)/(2) \rho[(r_1^4v_1^2)/(r_2^4) - v_1^2]\\\\P_1 = P_2 + (1)/(2) \rho v_1^2[(r_1^4)/(r_2^4) - 1]\\\\P_1 = 1.01*10^5 + (1)/(2)* 1000* 0.75^2[((0.018)^4)/((0.0053)^4) - 1]\\\\P_1 = 1.01*10^5 + (1)/(2)* 1000* 0.75^2(132.04)\\\\P_1 = 1.01*10^5 +37136.25 \\\\P_1 = 1.38 *10^5 \ Pa`

Therefore, the absolute pressure of the water in the pipe is 1.38 x 10⁵ Pa