Question

A company is producing two types of ski goggles. Thirty percent of the production is of type A, and the rest is of type B. Five percent of all type A goggles are returned within 10 days after the sale, whereas only two percent of type B are returned. If a pair of goggles is returned within the first 10 days after the sale, the probability that the goggles returned are of type B is:

Answer 1

The required probability is 0.4828.

Explanation:

We are given that a company is producing two types of ski goggles. Thirty percent of the production is of type A, and the rest is of type B.

Five percent of all type A goggles are returned within 10 days after the sale, whereas only two percent of type B are returned.

Let the probability that production is of Type A = P(A) = 30%

Probability that production is of Type B = P(B) = 1 - P(A) = 1 - 0.30 = 70%

Also, let R = event that pair of goggles are returned

So, the probability that type A goggles are returned within 10 days after the sale = P(R/A) = 5%

Probability that type B goggles are returned within 10 days after the sale = P(R/B) = 2%

Now, given a pair of goggles is returned within the first 10 days after the sale, the probability that the goggles returned are of type B is given by = P(B/R)

We will use the concept of Bayes' Theorem to calculate the above probability.

So, P(B/R) =
`(P(B) * P(R/B))/(P(A) * P(R/A)+P(B) * P(R/B))`

=
`(0.70 * 0.02)/(0.30 * 0.05+0.70 * 0.02)`

=
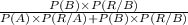
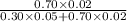
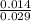`(0.014)/(0.029)` = 0.4828