Question

Which of the following shows the extraneous solution to the logarithmic equation log Subscript 7 Baseline (3 x cubed + x) minus log Subscript 7 Baseline (x) = 2 x = negative 16 x = negative 4 x = 4 x = 16

Answer 1

x = - 4

Explanation:

Got it right :)

Answer 2

• x = -4

Explanation:

A graphing calculator shows there is one solution to ...

`\log_7{(3x^2+x)}-\log_7{(x)}=2`

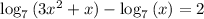
However, the usual solution method would be to combine the logarithms and take the antilog to get ...

`\log_7{\left((3x^3+x)/(x)\right)}=2\\\\\log_7{(3x^2 +1)}=2\\\\3x^2+1=7^2\\\\x^2=(49-1)/(3)=16\\\\x=\pm 4\qquad\text{take the square root}`

This gives two solutions. the "solution" x = -4 is extraneous, as it doesn't work in the original equation. "x" must be positive in the log expressions.