Question

Find lim x→3 sqrt 2x+3-sqrt 3x/ x^2-3x. you must show your work or explain your work in words plsss I need help

Answer 1

I'm assuming the limit is supposed to be

`\displaystyle\lim_(x\to3)(√(2x+3)-√(3x))/(x^2-3x)`

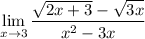
Multiply the numerator by its conjugate, and do the same with the denominator:

`\left(√(2x+3)-√(3x)\right)\left(√(2x+3)+√(3x)\right)=\left(√(2x+3)\right)^2-\left(√(3x)\right)^2=-(x-3)`

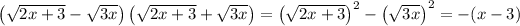
so that in the limit, we have

`\displaystyle\lim_(x\to3)(-(x-3))/((x^2-3x)\left(√(2x+3)+√(3x)\right))`

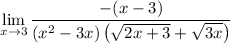
Factorize the first term in the denominator as

`x^2-3x=x(x-3)`

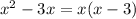
The
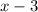`x-3` terms cancel, leaving you with

`\displaystyle\lim_(x\to3)(-1)/(x\left(√(2x+3)+√(3x)\right))`

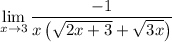
and the limand is continuous at
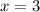`x=3`, so we can substitute it to find the limit has a value of -1/18.