Question

The froghopper, a tiny insect, is a remarkable jumper. Suppose a colony of the little critters is raised on Rhea, a moon of Saturn, where the acceleration due to gravity is only 0.264 m/s2 , whereas gravity on Earth is =9.81 m/s2 . If on Earth a froghopper's maximum jump height is ℎ and its maximum horizontal jump range is R, what would its maximum jump height and range be on Rhea in terms of ℎ and R? Assume the froghopper's takeoff velocity is the same on Rhea and Earth.

Answer 1

Maximum height of jump on Rhea is 37.16 times of that on Earth, i.e 37.16h

Maximum range of jump on Rhea is 37.16 of times that on Earth, i.e 37.16R

Step-by-step explanation:

The acceleration due to gravity on Rhea = 0.264 m/s^2

Acceleration due to gravity on earth here = 9.81 m/s^2

this means that the acceleration due to gravity g on earth is 9.81/0.264 = 37.16 times that on Rhea.

maximum height that can be achieved by the froghopper is given by the equation;

h =
`(u^(2)sin^(2) \alpha)/(2g)`

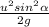
let us put all the numerator of the equation as k, since the velocity of take off is the same for Earth and Rhea. The equation is simplified to

h =
`(k)/(2g)`

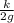
for earth,

h =
`(k)/(2*9.81)` =
`(k)/(19.62)`

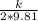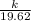
for Rhea,

h =
`(k)/(2*0.264)` =
`(k)/(0.528)`

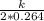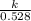
therefore,

h on Rhea is
`(k)/(0.528)` ÷
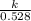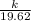`(k)/(19.62)` = 37.16 times of that on Earth, i.e 37.16h

Equation for range R is given as

R =
`(u^(2)sin 2\alpha)/(g)`

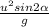
following the same approach as before,

R on Rhea will be
`(k)/(0.264)` ÷
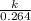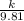`(k)/(9.81)` = 37.16 of times that on Earth, i.e 37.16R