Question

Could someone please help me with the steps for this problem? Factor by grouping: w²+3w+w+3

Answer 1

Please see steps below

Explanation:

In order to factor by grouping, we divide the four terms given into two groups, and extract on each group any common factor we can.

In our example, we can select the terms:
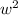`w^2` and
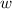`w` as one of our groups, and
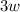`3w` and 3 in the other group. Then we re-organize the expression as:

`(w^2+w)+(3x+3)`

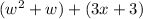
Now we extract from the first binomial group, the factor
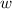`w` as a common factor of both terms, and from the second group we extract the factor "3" as common factor of those two terms:

`(w^2+w)+(3x+3)\\w(w+1)+3(w+1)`

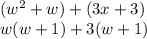
We notice now that after the extraction, we are left with two exactly equal binomial factors
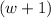`(w+1)` that appeared in the first group and in the second group. We proceed then to extract it as common factor for the two groups:

`w(w+1)+3(w+1)\\(w+1)(w+3)`

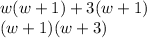
this last product of two binomials (
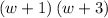`(w+1)\,(w+3)` is the result of factoring the original expression.