Question

Consider a car owner who has an 80% chance of no accidents in a year, a 20% chance of being in a single accident in a year, and no chance of being in more than one accident in a year. For simplicity, assume that there is a 50% probability that after the accident the car will need repairs costing $500, a 40% probability that the repairs will cost $5,000, and a 10% probability that the car will need to be replaced, which will cost $15,000. What is the expected loss for the car owner per year

Answer 1

The expected loss for the car owner per year is $750.

Explanation:

We are given that a car owner who has an 80% chance of no accidents in a year, a 20% chance of being in a single accident in a year, and no chance of being in more than one accident in a year.

Let X = Loss for the particular year for a car owner

Now as we know that the loss to the car owner may be of $0, $500, $5,000 or $15,000 because these amount he has to pay as a part of repair cost if his car met with an accident.

So, the probability distribution of X is given by;

X (Amount of Loss) P(X)

$0 0.80

$500 (0.20)(0.50) = 0.10

$5,000 (0.20)(0.40) = 0.08

$15,000 (0.20)(0.10) = 0.02

Total 1

Here, the probability of (0.20)(0.50) means that for the loss of $500, first the car must have to met with an accident and then there is 50% chance that after the accident the car will need repairs costing $500.

Now, the expected loss for the car owner per year is =
`\sum (X * P(X))`

`\sum (X * P(X))` =
`(0 * 0.80) + (500 * 0.10)+(5,000 * 0.08)+(15,000 * 0.02)`

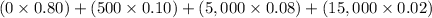
= 50 + 400 + 300 = $750.

So, the expected loss for the car owner per year is $750.