Answer:
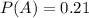
We want to find the probability that a randomly selected freshman from this college does not take an introductory statistics class, so then we can use the complement rule given by:
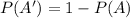
Where A is the event of interest (a freshman at a certain college takes an introductory statistics class) and A' the complement (a freshman at a certain college NOT takes an introductory statistics class) and then replacing we got:

Explanation:
For this problem we know that the probability that a freshman at a certain college takes an introductory statistics class is 0.21, let's define of interest as A and we can set the probability like this:
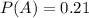
We want to find the probability that a randomly selected freshman from this college does not take an introductory statistics class, so then we can use the complement rule given by:
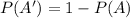
Where A is the event of interest (a freshman at a certain college takes an introductory statistics class) and A' the complement (a freshman at a certain college NOT takes an introductory statistics class) and then replacing we got:
