Answer:
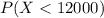
And for this case we can use the cumulative distribution function given by:
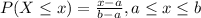
And using this formula we have this:
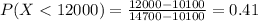
Then we can conclude that the probability that your bid will be accepted would be 0.41
Explanation:
Let X the random variable of interest "the bid offered" and we know that the distribution for this random variable is given by:
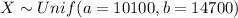
If your offer is accepted is because your bid is higher than the others. And we want to find the following probability:
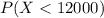
And for this case we can use the cumulative distribution function given by:
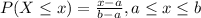
And using this formula we have this:
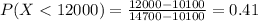
Then we can conclude that the probability that your bid will be accepted would be 0.41