Question

Part 3: Problem Set 1. An object is pulled by a rope and dragged to the right 12 meters across a rough surface. The tension in the rope is 105 N and the rope makes an angle of 35 degrees with the horizontal. The rough surface exerts a constant frictional force of 50 N as the object is dragged. 105 N 12 meters a) Find the total amount of work done on the object. Consider the following forces: tension, friction, gravity and normal. b) Use the work energy theorem to find the block's change in kinetic energy.

Answer 1

a) WT = 322.74 J

b) ΔK = 322.74J

Step-by-step explanation:

a) In order to calculate the total amount of work on the object you take into account the work done by the tension in the rope, the friction force of the surface and the gravitational force:

`W_T=W_p-W_f-W_g` (1)

WT: total work

Wp: work done by rope

Wf: work done by friction

Wg: work done by gravitational force

For each contribution to the total work you have:

For Wp:

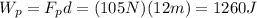`W_p=F_pd=(105N)(12m)=1260J` (2)

where d is the distance traveled by the object = 12m

For Wf:

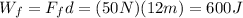`W_f=F_fd=(50N)(12m)=600J` (3)

For Wg:

`Wg=F_gd`

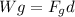
Fg is the incline horizontal component of the weight of the object, then you have:

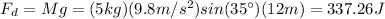`F_d=Mg=(5kg)(9.8m/s^2)sin(35\°)(12m)=337.26J` (4)

where g is the gravitational constant with value = 9.8m/s^2

Finally, you replace the results obtained in (2), (3) and (4), into the equation (1) for WT:

`W_T=1260J-600J-337.26J=322.74J`

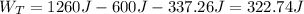
The total amount of work on the object is 322.74J

b) To find the change in the kinetic energy of the object you use the following formula:

`W_T=\Delta K`

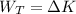
THen, the change in the kinetic energy is 322.74Ja