Answer:
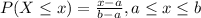
And using this formula we have this:
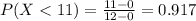
Then we can conclude that the probability that that a person waits fewer than 11 minutes is approximately 0.917
Explanation:
Let X the random variable of interest that a woman must wait for a cab"the amount of time in minutes " and we know that the distribution for this random variable is given by:
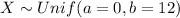
And we want to find the following probability:
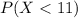
And for this case we can use the cumulative distribution function given by:
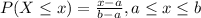
And using this formula we have this:
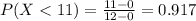
Then we can conclude that the probability that that a person waits fewer than 11 minutes is approximately 0.917