Suppose 43% of the population has a retirement account. If a random sample of size 774 is selected, what is the probability that the proportion of persons with a retirement account will differ from the population proportion by less than 3%?
Answer:
the probability that the proportion of persons with a retirement account will differ from the population proportion by less than 3% is 0.9082
Explanation:
Given that:
sample size n = 774
Let P be the population proportion for having a retirement account = 0.43
Also
Let consider
 be the sample proportion of having a retirement account.
be the sample proportion of having a retirement account.
However; as n is > 30 ; we can say:
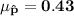 ;
;
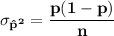
⇒
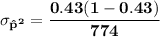
⇒
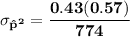
So; we need P( the sample proportion will differ from 'p' by less than 3% i.e 0.03)
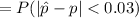
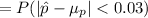

![= P(|Z|<1.6859)\ \ \ \ [Z=((\hat P - \mu_(\hat P))/(\sigma_(\hat P))) \sim N(0,1)]](https://img.qammunity.org/2021/formulas/mathematics/college/mwtvr978e2ks2d3ci17kew2s6r9mozwh64.png)
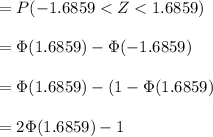
From Normal Cumulative Distribution Function Table

= 1.9082 - 1
= 0.9082
Thus; the probability that the proportion of persons with a retirement account will differ from the population proportion by less than 3% is 0.9082