Question

What is the simplified form of the expression? 6/√5−√2

Answer 1

The expression can be simplified into
`2\,√(5) +2√(2)`

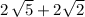
with no square roots in the denominator

Explanation:

We are considering the expression
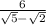`(6)/(√(5)-√(2) )` which I believe is what you wanted to type in your question.

The idea behind simplification of the expression, is normally associated with the rationalization of the denominator by eliminating irrational numbers from it. This means to get rid of any "irrational" number expression (like in this example, the square root of non-perfect square numbers (
`√(5)\,\,\,and \,\,√(2)`).

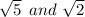We proceed by writing this quotient in an equivalent form by multiplying its numerator and its denominator by what is called the "conjugate" of the denominator. In our case, multiply by "
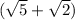`(√(5) +√(2))` ", because such product will allow the denominator to become a rational number:

`(6)/(√(5)-√(2) )\,*\,((√(5)+√(2) ))/((√(5)+√(2)) ) =(6\,(√(5)\,+\,√(2) ))/(√(5)^2-√(2)^2 )=(6\,(√(5)\,+\,√(2) ))/(3)=2\,√(5) +2√(2)`

where we find all square roots eliminated from the denominator