Question

The breaking strength of a rivet has a mean of 10,000 psi and a standard deviation of 714.2857 psi. What is the probability that the sample mean breaking strength for a random sample of 49 rivets is between 9,832 and 10,200?

Answer 1

`z= (9832- 10000)/((714.2857)/(√(49)))= -1.646`

`z= (10200- 10000)/((714.2857)/(√(49)))= 1.96`

And we can use the normal standard distribution table or excel and we can find the probability with this difference:

`P(-1.646 <z< 1.96) =P(z<1.96) -P(z<-1.646) =0.975-0.0499= 0.9251`

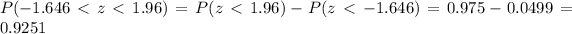
Then the probability that the sample mean breaking strength for a random sample of 49 rivets is between 9,832 and 10,200 is 0.9251

Explanation:

For this case we have the following info given:

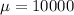`\mu = 10000` represent the mean

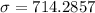`\sigma = 714.2857` represent the deviation

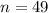`n = 49` represent the sample size selected

For this case since the sample size is large enough n>30 we have enough evidence to use the central llmit theorem and the distribution for the sample mena would be given by:

`\bar X \sim N(\mu,(\sigma)/(√(n)))`

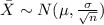
And we want to find the following probability:

`P(9832 < \bar X< 10200)`

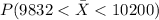
And we can use the z score formula given by:

`z = (\bar X -\mu)/((\sigma)/(√(n)))`

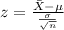
And if we use the z score formula for the limits given we got:

`z= (9832- 10000)/((714.2857)/(√(49)))= -1.646`

`z= (10200- 10000)/((714.2857)/(√(49)))= 1.96`

And we can use the normal standard distribution table or excel and we can find the probability with this difference:

`P(-1.646 <z< 1.96) =P(z<1.96) -P(z<-1.646) =0.975-0.0499= 0.9251`

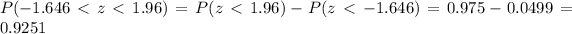
Then the probability that the sample mean breaking strength for a random sample of 49 rivets is between 9,832 and 10,200 is 0.9251