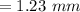Question

A rectangular bar of length L has a slot in the central half of its length. The bar has width b, thickness t, and elastic modulus E. The slot has width b/3. The overall length of the bar is L = 570 mm, and the elastic modulus of the material is 77 GPa. If the average normal stress in the central portion of the bar is 200 MPa, calculate the overall elongation δ of the bar.

Answer 1

The correct answer to the following question will be "1.23 mm".

Step-by-step explanation:

The given values are:

Average normal stress,

`\sigma=200 \ MPa`

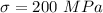
Elastic module,

`E = 77 \ GPa`

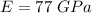
Length,

`L = 570 \ mm`

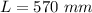
To find the deformation, firstly we have to find the equation:

⇒
`\delta=\Sigma(N_(i)L_(i))/(E \ A_(i))`

⇒
`=(P((L)/(H)))/(E(bt)) +(P((L)/(2)))/(E (bt)((2)/(3)))+(P((L)/(H)))/(Ebt)`

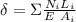
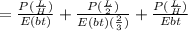
On taking "
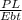`(PL)/(Ebt)`" as common, we get

⇒
`=((PL)/(Ebt))/([(1)/(4)+(3)/(4)+(1)/(4)])`

⇒
`=(5PL)/(HEbt)`

Now,

The stress at the middle will be:

⇒
`\sigma=(P)/(A)`

⇒
`=(P)/(((2)/(3))bt)`

⇒
`=(3P)/(2bt)`

⇒
`(P)/(bt) =(2 \sigma)/(3)`

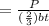
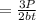
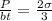
Hence,

⇒
`\delta=(5 \sigma \ L)/(6E)`

On putting the estimated values, we get

⇒
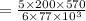
`=(5* 200* 570)/(6* 77* 10^3)`

⇒
`=(570000)/(462000)`

⇒
`=1.23 \ mm`