Answer:
The approximate probability that more than six students were born on Christmas day is P=0.105.
Explanation:
This can be modeled as a binomial variable, with n=1460 and p=1/365.
The sample size n is the total amount of students and the probability of success p is the probability of each individual of being born on Christmas day.
As the sample size is too large to compute it as a binomial random variable, we approximate it to the normal distribution with the following parameters:
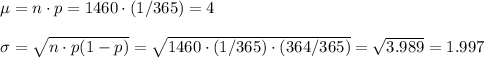
We want to calculate the probability that more than 6 students were born on Christmas day. Ww apply the continuity factor and we write the probability as:
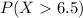
We calculate the z-score for X=6.5 and then calculate the probability:
