Question

You throw a small ball upward and notice the time it takes to come back. If you then throw the same ball so that it takes twice as much time to come back, what is true about the motion of the ball the second time?(a) Its initial speed was twice the speed in the first experiment.(b) It traveled an upward distance that is twice the distance of the original toss.(c) It had twice as much acceleration on the way up as it did the first time.(d) The ball stopped at the highest point and had zero acceleration at that point.

Answer 1

(a) Its initial speed was twice the speed in the first experiment.

Step-by-step explanation:

In order to determine what means that in the second launching the flight time of the same ball is twice respect to the first launching, you use the following formula:

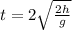`t=2\sqrt{(2h)/(g)}` (1)

h: height reached by the ball

g: gravitational constant

In the equation you take into account that t is the time that ball takes to go upward and go downward, that is the reason of the factor 2 before the square root.

Furthermore you use the fact that the maximum height reached by the ball is given by:

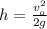`h=(v_o^2)/(2g)` (2)

Next, you replace the equation (2) into the equation (1):

`t=2\sqrt{(2v_o^2)/(2g^2)}=2(v_o)/(g)`

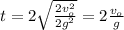
Then, you can notice that if the initial velocity is twice the flight time of the ball is also twice.

Hence, the anwser is:

(a) Its initial speed was twice the speed in the first experiment.