Question

In a hydraulic lift, if the pressure exerted on the liquid by one piston is increased by 100 N/m2 , how much additional weight can the other piston slowly lift if its cross sectional area is 25 m2

Answer 1

The additional weight and mass needed for lifting the other piston slowly is 2500 N and 254.92 kg, respectively.

Step-by-step explanation:

By means of the Pascal's Principle, the hydraulic lift can be modelled by the following two equations:

Hydraulic Lift - Before change

`P = (F)/(A)`

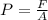
Hydraulic Lift - After change

`P + \Delta P = (F + \Delta F)/(A)`

Where:

`P` - Hydrostatic pressure, measured in pascals.

`\Delta P` - Change in hydrostatic pressure, measured in pascals.

`A` - Cross sectional area of the hydraulic lift, measured in square meters.

`F` - Hydrostatic force, measured in newtons.

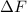`\Delta F` - Change in hydrostatic force, measured in newtons.

The additional weight is obtained after some algebraic handling and the replacing of all inputs:

`(F)/(A) + \Delta P = (F)/(A) + (\Delta F)/(A)`

`\Delta P = (\Delta F)/(A)`

`\Delta F = A\cdot \Delta P`

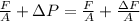
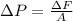
Given that
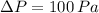`\Delta P = 100\,Pa` and
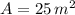`A = 25\,m^(2)`, the additional weight is:

`\Delta F = (25\,m^(2))\cdot (100\,Pa)`

`\Delta F = 2500\,N`

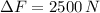
The additional mass needed for the additional weight is:

`\Delta m = (\Delta F)/(g)`

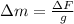
Where:

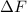`\Delta F` - Additional weight, measured in newtons.

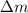`\Delta m` - Additional mass, measured in kilograms.

`g` - Gravitational constant, measured in meters per square second.

If
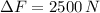`\Delta F = 2500\,N` and
`g = 9.807\,(m)/(s^(2))`, then:

`\Delta m = (2500\,N)/(9.807\,(m)/(s^(2)) )`

`\Delta m = 254.92\,kg`

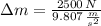
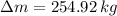
The additional weight and mass needed for lifting the other piston slowly is 2500 N and 254.92 kg, respectively.