Question

The wheels of a skateboard roll without slipping as it accelerates at 0.40 m/s2 down an 85-m-long hill. Part A If the skateboarder travels at 1.8 m/s at the top of the hill, what is the average angular speed of the 2.6-cm-radius wheels during the entire trip down the hill

Answer 1

average angular speed = 196.92 rad/s

Step-by-step explanation:

Given data

accelerates down = 0.40 m/s²

down hill travel = 85-m

travels top of hill = 1.8 m/s

radius wheels = 2.6 cm

Solution

We will apply here equation of motion that is express as

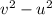`v^(2)-u^(2)` = 2as ...............1

here v is final velocity and u is final velocity and s is dispalement

so put here value we get first final velocity

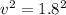`v^(2) = 1.8^(2)` + 2 × 0.40 × 85

solve it we get

`v^(2)` = 71.24

v = 8.44 m/s

and

initial angular speed is express as

initial angular speed ω =
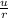`(u)/(r)` ............2

put here value

initial angular speed ω =
`(1.8)/(2.6 * 10^(-2))`

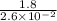
initial angular speed ω = 69.23 rad/s

and

final angular speed ω =
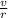`(v)/(r)` ..............3

put here value

final angular speed ω =
`(8.44)/(2.6 * 10^(-2))`

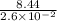
final angular speed ω = 324.61 rad/s

so now we get average of angular speed that is

average angular speed = ( 69.23 + 324.61 ) ÷ 2

average angular speed = 196.92 rad/s