Answer:
Due to the higher z-score, he did better on the SAT.
Explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Determine which test the student did better on.
He did better on whichever test he had the higher z-score.
SAT:
Scored 1070, so
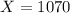
SAT scores have a mean of 950 and a standard deviation of 155. This means that
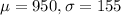 .
.

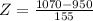

ACT:
Scored 25, so
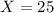
ACT scores have a mean of 22 and a standard deviation of 4. This means that
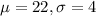

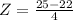
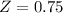
Due to the higher z-score, he did better on the SAT.