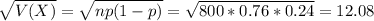Answer:
12.08
Explanation:
For each sunflower, there are only two possible outcomes. Either it germinates, or it does not. The probability of a sunflower germinating is independent of other sunflowers. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
The standard deviation of the binomial distribution is:
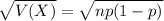
Seventy-six percent of sunflower seeds will germinate into a flower
This means that
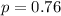
Samples of 800:
This means that
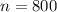
The standard deviation for the number of sunflower seeds that will germinate in such samples of size 800 is: