Question

3. Students arrive at an ATM machine in a random pattern with an average inter-arrival time of 3 minutes. The length of transactions at the ATM machine is exponentially distributed with an average of 2 minutes. (a) What is the probability that a student arriving at the ATM will have to wait

Answer 1

The probability that a student arriving at the ATM will have to wait is 67%.

Explanation:

This can be solved using the queueing theory models.

We have a mean rate of arrival of:

`\lambda=1/3\,min^(-1)`

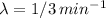
We have a service rate of:

`\mu=1/2\,min^(-1)`

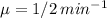
The probability that a student arriving at the ATM will have to wait is equal to 1 minus the probability of having 0 students in the ATM (idle ATM).

Then, the probability that a student arriving at the ATM will have to wait is equal to the utilization rate of the ATM.

The last can be calculated as:

`P_(n>0)=\rho=(\lambda)/(\mu)=(1/3)/(1/2)=(2)/(3)=0.67`

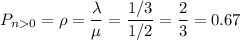
Then, the probability that a student arriving at the ATM will have to wait is 67%.