Question

3. Suppose the average amount of apples per tree in a large orchard is 600 pounds with a standard deviation of 70 pounds. a. Assuming the necessary conditions are satisfied, give the mean and standard deviation of the Normal model that would be used to approximate the sampling distribution of the sample mean for a sample of 40 trees. Include units in your answers. b. Sketch and clearly label the sampling model for a sample of 40 trees, based on the 68-95-99.7 Rule. c. Find the probability that a random sample of 40 trees has an average amount of apples of 620 pounds or higher. (To show your work: Write down which calculator/program you are using and what values you are entering into the calculator.)

Answer 1

a) The sampling distributio will be normal with mean 600 and standard deviation 11.07.

b) - 68% of the samples will have means between 589 and 611 apples per tree.

- 95% of the samples will have means between 578 and 622 apples per tree.

- 99.7% of the samples will have means between 567 and 633 apples per tree.

c) The probability that a random sample of 40 trees has an average amount of apples of 620 pounds or higher is 0.035.

Explanation:

a) The sampling distribution for a population with mean of 600 pounds and standard deviation of 70 pounds, with a sample size of 40 trees, will have the following parameters:

`\mu_s=\mu=600\\\\ \sigma_s=(\sigma)/(√(n))=(70)/(√(40))=(70)/(6.325)=11.07`

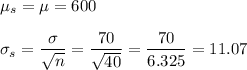
b) Using the 68-95-99.7 rule for the sampling distribution, we can tell that:

- 68% of the samples will have means between 589 and 611 apples per tree.

`X_1=\mu+z_1\cdot\sigma/√(n)=600-1\cdot 70√(40)=600-11=589\\\\X_2=\mu+z_2\cdot\sigma/√(n)=600+1\cdot 70√(40)=600+11=611`

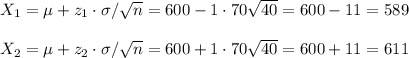
- 95% of the samples will have means between 578 and 622 apples per tree.

`X_1=\mu+z_1\cdot\sigma/√(n)=600-2\cdot 70√(40)=600-22=578\\\\X_2=\mu+z_2\cdot\sigma/√(n)=600+2\cdot 70√(40)=600+22=622`

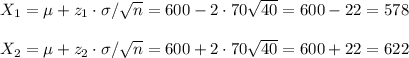
- 99.7% of the samples will have means between 567 and 633 apples per tree.

`X_1=\mu+z_1\cdot\sigma/√(n)=600-3\cdot 70√(40)=600-33=567\\\\X_2=\mu+z_2\cdot\sigma/√(n)=600+3\cdot 70√(40)=600+33=633`

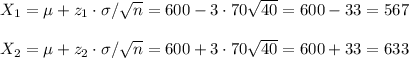
c) We can calculate the probability with the z-score for X=620.

`z=(X-\mu)/(\sigma/√(n))=(620-600)/(70/√(40))=(20)/(11.068)=1.807\\\\\\P(X>620)=P(z>1.807)=0.035`

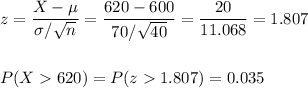
The probability that a random sample of 40 trees has an average amount of apples of 620 pounds or higher is 0.035.