Question

A quantity of 0.0250 mol of a gas initially at 0.050 L and 19.0°C undergoes a constant-temperature expansion against a constant pressure of 0.200 atm. If the gas is allowed to expand unchecked until its pressure is equal to the external pressure, what would its final volume be before it stopped expanding, and what would be the work done by the gas?

Answer 1

`V_2=2.995L\\\\W=248.5J`

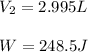
Step-by-step explanation:

Hello,

In this case, for us to compute the final volume we apply the Boyle's law that analyzes the pressure-volume temperature as an inversely proportional relationship:

`P_1V_1=P_2V_2`

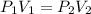
So we solve for
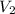`V_2` by firstly computing the initial pressure:

`P_1=(nRT)/(V_1)=(0.025mol*0.082(atm*L)/(mol*K)*(19+273.15)K)/(0.050L) =11.98atm`

`V_2=(P_1V_1)/(P_2)=(11.98atm*0.050L)/(0.200atm)\\ \\V_2=2.995L`

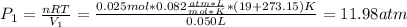
Finally, we can compute the work by using the following formula:

`W=nRTln((V_2)/(V_1) )=0.025mol*8.314(J)/(mol*K)*(19.0+273.15)K*ln((2.995L)/(0.050L)) \\\\W=248.5J`

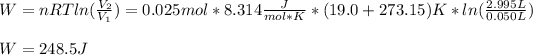
Best regards.