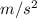Question

A rocket car on a horizontal rail has an initial mass of 2500 kg and an additional fuel mass of 1000 kg. At time t0 the rocket motor is ignited and the rocket burns fuel at a rate of 95 kg/s. The exit speed of the exhaust gas relative to the rocket is 2900 m/s. Neglecting drag and friction forces, determine the acceleration and the velocity of the car at time t = 10 s. Plot the acceleration and velocity from time t0 to t = 10 s.

Answer 1

Answer: Acceleration of the car at time = 10 sec is 108
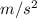`m/s^(2)` and velocity of the car at time t = 10 sec is 918.34 m/s.

Step-by-step explanation:

The expression used will be as follows.

`M(dv)/(dt) = u(dM)/(dt)`

`\int_{t_(o)}^{t_(f)} (dv)/(dt) dt = u\int_{t_(o)}^{t_(f)} (1)/(M) (dM)/(dt) dt`

=
`u\int_{M_(o)}^{M_(f)} (dM)/(M)`

`v_(f) - v_(o) = u ln (M_(f))/(M_(o))`

`v_(o) = 0`

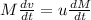
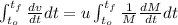
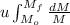
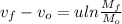
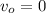
As,
`v_(f) = u ln ((M_(f))/(M_(o)))`

u = -2900 m/s

`M_(f) = M_(o) - m * t_(f)`

=
`2500 kg + 1000 kg - 95 kg * t_(f)s`

=
`(3500 - 95t_(f))s`

`v_(f) = -2900 ln((3500 - 95 t_(f))/(3500)) m/s`

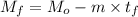
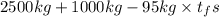
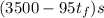
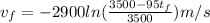
Also, we know that

a =
`(dv_(f))/(dt_(f)) = (u)/(M) (dM)/(dt)`

=
`(u)/(3500 - 95 t) * (-95) m/s^(2)`

=
`(95 * 2900)/(3500 - 95t) m/s^(2)`

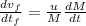
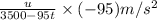
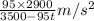
At t = 10 sec,

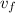`v_(f)` = 918.34 m/s

and, a = 108
`m/s^(2)`