Answer : The correct statements are,
AC = 5 cm
BA = 4 cm
The perimeter of triangle ABC is 12 cm.
Step-by-step explanation :
As we know that a, b, and c are midpoints of the sides of right triangle that means midpoint divide the side in equal parts.
Now we have to calculate the sides of triangle ABC by using Pythagoras theorem.
Using Pythagoras theorem in ΔACF :
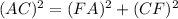
Now put all the values in the above expression, we get the value of side AC.

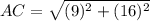
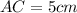
Using Pythagoras theorem in ΔDAB :
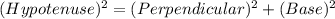
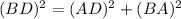
Now put all the values in the above expression, we get the value of side BA.
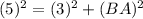
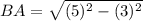
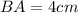
Using Pythagoras theorem in ΔBEC :
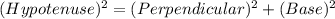
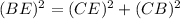
Now put all the values in the above expression, we get the value of side CB.
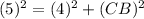
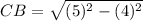
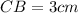
Now we have to calculate the perimeter of ΔABC.
Perimeter of ΔABC = Side AB + Side CB+ Side AC
Perimeter of ΔABC = 4 + 3 + 5
Perimeter of ΔABC = 12 cm
Now we have to calculate the area of ΔABC.
Area of ΔABC =
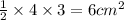
Now we have to calculate the area of ΔDEF.
Area of ΔDEF =
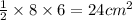
Area of ΔABC =
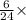 Area of ΔDEF
Area of ΔDEF
Area of ΔABC =
 Area of ΔDEF
Area of ΔDEF