Question

The area of the entire figure below is 1 square unit. How can we describe the area of the striped rectangle?

Answer 1

The area of the striped rectangle in the entire figure is
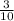`(3)/(10)` square units.

To describe the area of the striped rectangle, you can evaluate the expression:

`\left((1)/(5)+(1)/(5)\right) *\left((1)/(4)+(1)/(4)+(1)/(4)\right)`

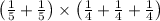
Let's simplify this expression step by step:

Simplify the terms within each set of parentheses:

`\left((2)/(5)\right) *\left((3)/(4)\right)`

Multiply the numerators and denominators:

`(2 * 3)/(5 * 4)`

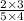
Simplify the fraction:

`(6)/(20)`

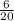
Reduce the fraction, if possible:

`(3)/(10)`

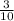
Therefore, the area of the striped rectangle is
`(3)/(10)` square units.

Answer 2

0.267 square units (or 8/30 square units)

Explanation:

width = 3 rectangles

length = 10 rectangles (left to right)

area = width * length = 30 rectangles

the striped rectangle is made up of 8 regular rectangles

thus, (area we want) / (total area) = 8/30 of the whole ≈ 0.267 of the whole

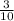the whole is 1 square unit, so 0.267 of 1 square unit = 0.267 * 1 square unit = 0.267 square units