Question

The scores on the Wechsler Adult Intelligence Scale are approximately Normal with \muμ = 100 and \sigmaσ = 15. If you scored 130, your score would be higher than approximately what percent of adults?

Answer 1

Your score would be higher than 97.72% of adults, that is, higher than approximately 98% of adults.

Explanation:

When the distribution is normal, we use the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this question, we have that:

`\mu = 100, \sigma = 15`

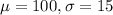
If you scored 130, your score would be higher than approximately what percent of adults?

To find the proportion of scores that are lower than, we find the pvalue of Z when X = 130. So

`Z = (X - \mu)/(\sigma)`

`Z = (130 - 100)/(15)`

`Z = 2`

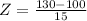
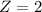
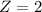`Z = 2` has a pvalue of 0.9772

0.9772*100 = 97.72%.

Your score would be higher than 97.72% of adults, that is, higher than approximately 98% of adults.