Question

One Sunday, 120 days before Christmas, Aldsworth store publishes an advertisement saying ‘120 shopping days until Christmas'. Aldsworth subsequently publishes similar advertisements every Sunday until Christmas. a. How many times does Aldsworth advertise? b. Find the sum of the numbers of days published in all the advertisements. c. On which day of the week is Christmas?

Answer 1

(a)18

(b)1089

(c)Sunday

Explanation:

The problem presented is an arithmetic sequence where:

• First Sunday, a=1
• Common Difference (Every subsequent Sunday), d=7

We want to determine the number of Sundays in the 120 days before Christmas.

(a)In an arithmetic sequence:

`\text{The nth term}, T_n=a+(n-1)d\\T_n \leq 120\\$Therefore:$\\1+7(n-1) \leq 120\\1+7n-7\leq 120\\7n-6\leq 120\\7n\leq 120+6\\7n\leq 126\\$Divide both sides by 7$\\n\leq 18`

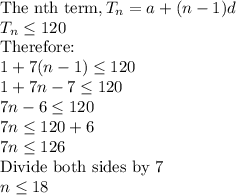
Since the result is a whole number, there are 18 Sundays in which Aldsworth advertises.

Therefore, Aldsworth advertised 18 times.

(b)Next, we want to determine the sum of the first 18 terms of the sequence

1,8,15,...

`\text{Sum of a sequence}, S_n=(n)/(2)( 2a+(n-1)d)\\S_(18)=(18)/(2)( 2*1+(18-1)*7)\\=9(2+17*7)\\=9(2+119)\\=9*121\\S_(18)=1089`

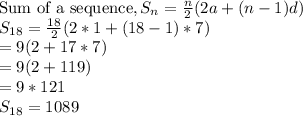
The sum of the numbers of days published in all the advertisements is 1089.

(c)SInce the 120th day is the 18th Sunday, Christmas is on Sunday.