Answer:
A) 0.028
Explanation:
Given:
Sample size, n = 115
Population parameter, p = 0.1
The X-Bin(n=155, p=0.1)
Required:
Find the standard deviation of the normal curve that can be used to approximate the binomial probability histogram.
To find the standard deviation, use the formula below:
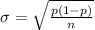
Substitute figures in the equation:
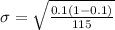

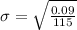
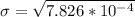
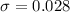
The Standard deviation of the normal curve that can be used to approximate the binomial probability histogram is 0.028