Question

A recent study claims that business travelers spend an average of $39 per day for meals. A sample of 15 business travelers found that they had spent an average of $42 per day with a standard deviation of $3.78. If α=0.05, what is the test value?

Answer 1

The test statistic value 't' = 3.074

Explanation:

Step(i):-

Given sample size 'n' = 15

mean of the Population 'μ' = $39

mean of the sample x⁻ = $42

standard deviation of the sample 's' = $3.78

Degrees of freedom ν = n-1 = 15-1 =14

`t_{(\alpha )/(2) } = 1.769`

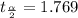
Null hypothesis : There is no significance difference between the means

H₀ : x⁻ = 'μ'

Alternative hypothesis : There is significance difference between the means

H₀ : x⁻ ≠ 'μ'

Test statistic

`t = (x^(-) -mean)/((s)/(√(n) ) )`

`t = (42 -39)/((3.78)/(√(15) ) )`

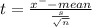
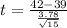
t = 3.074

The test value of t-statistic t = 3.074

The calculated value t = 3.074 > 1.769 at 0.05 level of significance

null hypothesis is rejected

Alternative hypothesis is accepted

Final answer:-

There is significance difference between the means