Answer:
i)
The probability that getting one heads and two tails = 0.375 = 37.5%
ii)
The probability that getting Exactly two heads = 0.375 = 37.5%
iii)
The probability that getting at -least two tails = 0.5 =50%
iv)
The probability that getting no heads = 0.125 = 12.5%
Explanation:
Explanation:-
Given Three coins are tossed
The number of exhaustive cases
= { HHH,TTT,HTT,THT,TTH,HTH,THH,HHT} =8
n(S) = 8
i)
Let 'E₁' be the event of getting one heads and two tails
n ( E₁) = {HTT ,THT , TTH} = 3
The probability that getting one heads and two tails
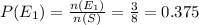
The chance of tossing one heads and two tails = 37.5%
ii)
Let 'E₂' be the event of getting Exactly two heads
n(E₂) = {HTH,THH,HHT} =3
The probability that getting Exactly two heads

The chance of tossing Exactly two heads = 37.5%
iii)
Let 'E₃' be the event of getting at -least two tails
n(E₃) = {TTT,HTT,THT,TTH} = 4
The probability that getting at -least two tails
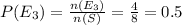
The chance of tossing at -least two tails = 50%
iv)
Let 'E₄' be the event of getting no heads
n(E₄) = { TTTT} =1
The probability that getting no heads
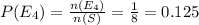
The chance of tossing no heads = 12.5%