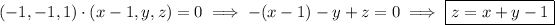Question

Find an equation for the plane that is tangent to the surface z equals ln (x plus y )at the point Upper P (1 comma 0 comma 0 ).

Answer 1

Let
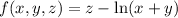`f(x,y,z)=z-\ln(x+y)`. The gradient of
`f` at the point (1, 0, 0) is the normal vector to the surface, which is also orthogonal to the tangent plane at this point.

So the tangent plane has equation

`\\abla f(1,0,0)\cdot(x-1,y,z)=0`

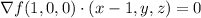
Compute the gradient:

`\\abla f(x,y,z)=\left((\partial f)/(\partial x),(\partial f)/(\partial y),(\partial f)/(\partial z)\right)=\left(-\frac1{x+y},-\frac1{x+y},1\right)`

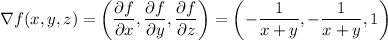
Evaluate the gradient at the given point:

`\\abla f(1,0,0)=(-1,-1,1)`

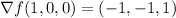
Then the equation of the tangent plane is

`(-1,-1,1)\cdot(x-1,y,z)=0\implies-(x-1)-y+z=0\implies\boxed{z=x+y-1}`