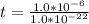Question

C2B.7Suppose I drop a 60-kg anvil from rest and from such a height that the anvil reaches a speed of 10 m/s just before hitting the ground. Assume the earth was at rest before I dropped the anvil. (a) What is the earth's speed just before the anvil hits

Answer 1

Complete Question

C2B.7

Suppose I drop a 60-kg anvil from rest and from such a height that the anvil reaches a speed of 10 m/s just before hitting the ground. Assume the earth was at rest before I dropped the anvil.

(a) What is the earth's speed just before the anvil hits?

b) How long would it take the earth to travel
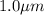`1.0 \mu m` (about a bacterium's width) at this speed?

Answer:

a

`|v_1| = 1.0*10^(-22) \ m/s`

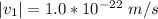
b

`t = 9.95 *10^(15) \approx 10 *10^(15) \ s`

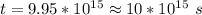
Step-by-step explanation:

From the question we are told that

The mass of the anvil is
`m_a = 60\ kg`

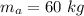
The speed at which it hits the ground is
`v = 10 \ m/s`

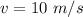
Generally the mass of the earth has a value
`m_e = 5972*10^(24) \ kg`

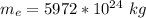
Now according to the principle of momentum conservation

`P_i = P_f`

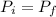
Where
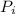`P_i` is the initial momentum which is zero given that both the anvil and the earth are at rest

Now
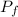`P_f` is the final momentum which is mathematically represented as

`P_f = m_a * v + m_e * v_1`

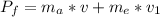
So

`0 = m_a * v + m_e * v_1`

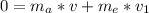
substituting values

`0 = 60 * 10 + 5.972 *10^(24) * v_1`

=>
`v_1 = -1.0*10^(-22) \ m/s`

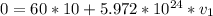
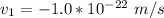
Here the negative sign show that it is moving in the opposite direction to the anvil

The magnitude of the earths speed is

`|v_1| = 1.0*10^(-22) \ m/s`

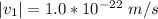
The time it would take the earth is mathematically represented as

`t = (d)/(|v_1|)`

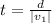
substituting values

`t = (1.0*10^(-6))/(1.0 *10^(-22))`

`t = 10 *10^(15) \ s`